



Next: Generalized a,b-Fibonacci numbers (this
Up: k-Fibonacci-q numbers and new
Previous: Definitions
Contents
Done by strong mathematical induction on 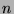 .
.
Base Case:
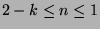 . WTS:
. WTS:
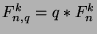 .
.
If
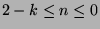 , then
, then 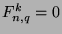 and
and 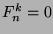 . Otherwise,
. Otherwise,  ,
so
,
so 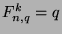 and
and 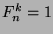 , so all cases are true.
, so all cases are true.
Induction Step: Assume for all 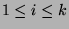 , that
, that
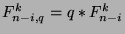 .
.
WTS:
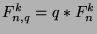 .
.
We can add the given from 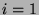 to
to  to get that
to get that
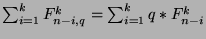 , or that
, or that
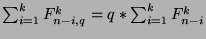 . By the definition of the sequences,
these collapse to
. By the definition of the sequences,
these collapse to
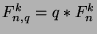 , which is what we wanted to show.
, which is what we wanted to show.
We will prove this by showing that 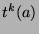 satisfies the definition of
satisfies the definition of 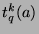 .
.
Part 1: WTS: 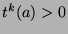 .
.
This is a property included in the definition of 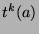 .
.
Part 2: WTS: For all  between
between 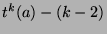 and
and 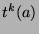 , inclusive,
, inclusive,
 .
.
Let  be between
be between 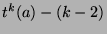 and
and 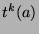 , inclusive. By the definition of
, inclusive. By the definition of
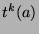 ,
,
 . Thus, by Theorem 35,
. Thus, by Theorem 35,
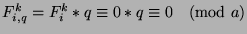 (since
(since
 by
definition of
by
definition of 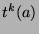 ), which is what we wanted to show.
), which is what we wanted to show.
Part 3: WTS:
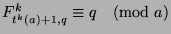 .
.
By the definition of 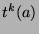 ,
,
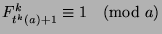 . Thus, by Theorem
35,
. Thus, by Theorem
35,
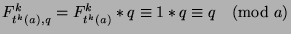 , which is what we
wanted to show.
, which is what we
wanted to show.
Part 4: WTS: If 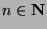 and
and 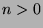 and for all
and for all  such that
such that
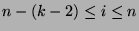 , it follows that
, it follows that
 and also
and also
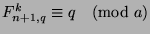 , then
, then 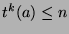 .
.
First, note that since 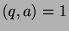 , then by Fact 5, there exists integers
, then by Fact 5, there exists integers
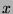 and
and 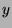 such that
such that 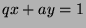 , so
, so 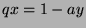 , so
, so
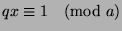 (by the definition
of mod). Now, let
(by the definition
of mod). Now, let
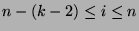 , so by Theorem 28,
, so by Theorem 28,
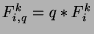 ,
so, multiplying both sides by
,
so, multiplying both sides by 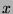 , we find that
, we find that
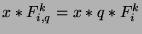 , or
, or
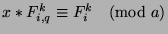 . Now, since
. Now, since
 , then
, then
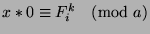 , or
, or
 . Similarly,
. Similarly,
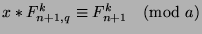 , and
, and
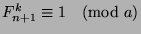 . Now by Theorem
24,
. Now by Theorem
24, 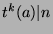 , so by Fact 3,
, so by Fact 3, 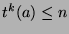 , which is what we wanted to
show.
, which is what we wanted to
show.
Part 1: WTS: If 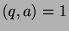 and
and
 , then
, then
 .
.
By Theorem 35,
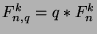 , so
, so
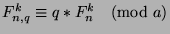 . Since
. Since
 , then
, then
 , or
, or
 , which is
what we wanted to show.
, which is
what we wanted to show.
Part 2: WTS: If 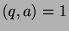 and
and
 , then
, then
 .
.
By Theorem 35,
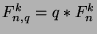 , so
, so
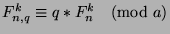 . Since
. Since
 , then
, then
 . Since
. Since 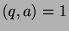 , by Fact 14
, by Fact 14
 , which is what we wanted to show.
, which is what we wanted to show.
We will prove this by showing that 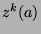 satisfies the properties of
satisfies the properties of 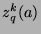 .
.
Part 1: WTS: 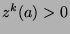 .
.
This is a property in the definition of 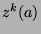 .
.
Part 2: WTS: For all  between
between 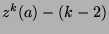 and
and 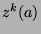 ,
inclusive,
,
inclusive,
 .
.
Let  be between
be between 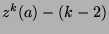 and
and 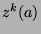 , inclusive. We know that
, inclusive. We know that
 , since this is a property in the definition of
, since this is a property in the definition of 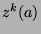 .
So, since
.
So, since 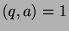 , by Theorem 37,
, by Theorem 37,
 , which is what we wanted to show.
, which is what we wanted to show.
Part 3: WTS: If, for all  between
between 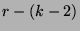 and
and 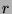 , inclusive,
it follows that
, inclusive,
it follows that
 and
and 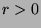 , then
, then 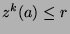 .
.
Let  be between
be between 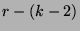 and
and 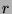 , inclusive. Since
, inclusive. Since 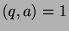 , by Theorem
37,
, by Theorem
37,
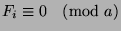 . So, this is true for all
. So, this is true for all  between
between 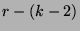 and
and 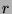 , so
by the definition of
, so
by the definition of 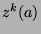 , it follows that
, it follows that 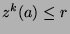 , which is what we wanted to show.
, which is what we wanted to show.
By Theorem 36,
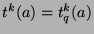 . By Theorem 37, the positions
of the zeros in the
. By Theorem 37, the positions
of the zeros in the 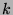 -Fibonacci sequence and the
-Fibonacci sequence and the 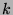 -Fibonacci-
-Fibonacci-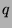 sequence are exactly the
same, so by the definition of
sequence are exactly the
same, so by the definition of 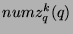 , it follows that
, it follows that
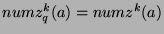 .
.
This will be proven by a construction. First, write down all 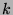 -Fibonacci-
-Fibonacci-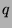 sequences from
the 1st term to the
sequences from
the 1st term to the 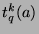 term modulo
term modulo 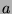 such that
such that 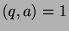 and
and
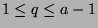 . Note
that the
number of such sequences is just
. Note
that the
number of such sequences is just 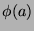 . Now, by Theorem 36, each of these
sequences is the same length, and by Theorem 37, all positions
that have
. Now, by Theorem 36, each of these
sequences is the same length, and by Theorem 37, all positions
that have 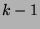 consecutive
consecutive 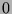 s will start at
the same position in every sequence. Now, consider terms whose position is of the form
s will start at
the same position in every sequence. Now, consider terms whose position is of the form
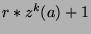 , where
, where 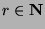 or
or  . These terms will be denoted by "
. These terms will be denoted by " terms". By
Theorem
38, these will all be after the only
places that have
terms". By
Theorem
38, these will all be after the only
places that have 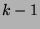 consecutive
consecutive 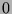 s in their sequences, and by Theorem 39,
there will be the same number of
s in their sequences, and by Theorem 39,
there will be the same number of  terms in each sequence. Now, we start with the first sequence
and look at all
terms in each sequence. Now, we start with the first sequence
and look at all  terms in that sequence. Then, we will search for a sequence in which any
terms in that sequence. Then, we will search for a sequence in which any
 term is equal to any
term is equal to any  term in the first sequence. Now, assume there is a
term in the first sequence. Now, assume there is a  term in the
term in the 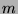 th line that is equal to some
th line that is equal to some  term in the
term in the 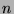 th line. Since all
th line. Since all
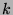 -Fibonacci-
-Fibonacci-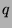 sequences are determined by
sequences are determined by 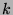 consecutive terms (like the
consecutive terms (like the 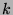 -Fibonacci
sequence), and all
-Fibonacci
sequence), and all  terms are preceded by
terms are preceded by 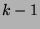
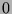 s, we can say
that these two sequences are in fact the same sequence shifted by
s, we can say
that these two sequences are in fact the same sequence shifted by 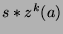 terms, where
terms, where 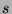 is some integer. So, all
is some integer. So, all  terms in the sequences will be the same. Therefore, we can
eliminate or cross out one of these sequences, while still keeping all numbers that were
terms in the sequences will be the same. Therefore, we can
eliminate or cross out one of these sequences, while still keeping all numbers that were  terms. Continue this until there are no more duplicate
terms. Continue this until there are no more duplicate  terms left. Now, we will show that
all
terms left. Now, we will show that
all  terms in all
terms in all 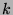 -Fibonacci-
-Fibonacci-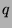 sequences (where
sequences (where 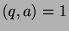 )
are relatively prime to
)
are relatively prime to 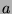 .
First, looking back at the proof of Theorem 27, we
established that
.
First, looking back at the proof of Theorem 27, we
established that
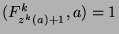 (since
(since
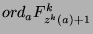 exists). Now,
Theorem 20 states that if, for all
exists). Now,
Theorem 20 states that if, for all  between
between 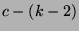 and
and 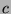 , inclusive,
it follows that
, inclusive,
it follows that
 , then
, then
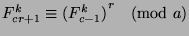 . We
can plug in
. We
can plug in 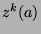 for
for 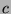 in
this formula to say that
in
this formula to say that
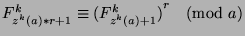 . Now,
since we know that
. Now,
since we know that
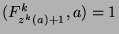 ,
by Fact 12 we can say that
,
by Fact 12 we can say that
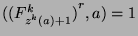 for all
for all 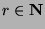 . We can reduce this to say that
. We can reduce this to say that
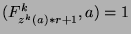 for all
for all 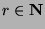 , which says that every
, which says that every
 term
in the
term
in the 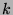 -Fibonacci sequence is relatively prime to
-Fibonacci sequence is relatively prime to 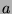 . Now, since we are considering every
. Now, since we are considering every
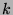 -Fibonacci-
-Fibonacci-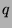 sequence such that
sequence such that 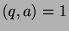 , by Fact 11 we can say that
, by Fact 11 we can say that
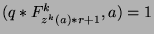 . By Theorem 35, these are just the
. By Theorem 35, these are just the  terms in all of the
terms in all of the 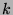 -Fibonacci-
-Fibonacci-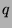 sequences,
so all
sequences,
so all  terms in every sequence listed are relatively prime to
terms in every sequence listed are relatively prime to 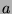 .
Notice that every sequence starts with a
.
Notice that every sequence starts with a  term, and since the first term of every
term, and since the first term of every
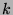 -Fibonacci-
-Fibonacci-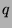 sequence is just
sequence is just 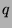 , we have started with all
relatively prime numbers less than
, we have started with all
relatively prime numbers less than
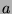 . Every time we eliminate a sequence, there is still at least 1 copy left of every number
relatively prime to
. Every time we eliminate a sequence, there is still at least 1 copy left of every number
relatively prime to 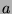 and less than
and less than 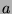 , since there are 2 copies of the same
, since there are 2 copies of the same  term in
each sequence, and only 1 is removed. If there is more than 1 copy left, we eliminate one of
the sequences, so after we are finished there is exactly 1 and only 1 copy of every number
less than
term in
each sequence, and only 1 is removed. If there is more than 1 copy left, we eliminate one of
the sequences, so after we are finished there is exactly 1 and only 1 copy of every number
less than 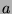 and relatively prime to
and relatively prime to 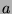 . Now, we will count the number of
. Now, we will count the number of  terms left in 2 different ways. By
the definition of
terms left in 2 different ways. By
the definition of 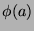 , there are exactly
, there are exactly 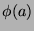
 terms left. Also, since every
sequence of
terms left. Also, since every
sequence of 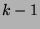 consecutive
consecutive 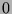 s
in each sequence corresponds to a
s
in each sequence corresponds to a  term (the
term (the 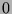 s ending in the
s ending in the 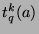 position
correspond to
the
position
correspond to
the  term in the first position), and there are
term in the first position), and there are 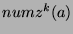 sequences of
sequences of 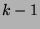 consecutive
consecutive 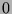 s in every sequence, we can say
that there are
s in every sequence, we can say
that there are 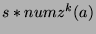
 terms, where
terms, where 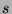 is the number of sequences left. So,
is the number of sequences left. So,
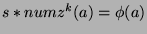 , or
, or
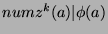 by the definition of divides.
by the definition of divides.




Next: Generalized a,b-Fibonacci numbers (this
Up: k-Fibonacci-q numbers and new
Previous: Definitions
Contents
Gregory Stoll
2000-04-08
![]() . WTS:
. WTS:
![]() .
.
![]() , then
, then ![]() and
and ![]() . Otherwise,
. Otherwise, ![]() ,
so
,
so ![]() and
and ![]() , so all cases are true.
, so all cases are true.
![]() , that
, that
![]() .
.
![]() .
.
![]() to
to ![]() to get that
to get that
![]() , or that
, or that
![]() . By the definition of the sequences,
these collapse to
. By the definition of the sequences,
these collapse to
![]() , which is what we wanted to show.
, which is what we wanted to show.
![]() .
.
![]() .
.
![]() between
between ![]() and
and ![]() , inclusive,
, inclusive,
![]() .
.
![]() be between
be between ![]() and
and ![]() , inclusive. By the definition of
, inclusive. By the definition of
![]() ,
,
![]() . Thus, by Theorem 35,
. Thus, by Theorem 35,
![]() (since
(since
![]() by
definition of
by
definition of ![]() ), which is what we wanted to show.
), which is what we wanted to show.
![]() .
.
![]() ,
,
![]() . Thus, by Theorem
35,
. Thus, by Theorem
35,
![]() , which is what we
wanted to show.
, which is what we
wanted to show.
![]() and
and ![]() and for all
and for all ![]() such that
such that
![]() , it follows that
, it follows that
![]() and also
and also
![]() , then
, then ![]() .
.
![]() , then by Fact 5, there exists integers
, then by Fact 5, there exists integers
![]() and
and ![]() such that
such that ![]() , so
, so ![]() , so
, so
![]() (by the definition
of mod). Now, let
(by the definition
of mod). Now, let
![]() , so by Theorem 28,
, so by Theorem 28,
![]() ,
so, multiplying both sides by
,
so, multiplying both sides by ![]() , we find that
, we find that
![]() , or
, or
![]() . Now, since
. Now, since
![]() , then
, then
![]() , or
, or
![]() . Similarly,
. Similarly,
![]() , and
, and
![]() . Now by Theorem
24,
. Now by Theorem
24, ![]() , so by Fact 3,
, so by Fact 3, ![]() , which is what we wanted to
show.
, which is what we wanted to
show.
![]() and
and
![]() , then
, then
![]() .
.
![]() , so
, so
![]() . Since
. Since
![]() , then
, then
![]() , or
, or
![]() , which is
what we wanted to show.
, which is
what we wanted to show.
![]() and
and
![]() , then
, then
![]() .
.
![]() , so
, so
![]() . Since
. Since
![]() , then
, then
![]() . Since
. Since ![]() , by Fact 14
, by Fact 14
![]() , which is what we wanted to show.
, which is what we wanted to show.
![]() .
.
![]() .
.
![]() between
between ![]() and
and ![]() ,
inclusive,
,
inclusive,
![]() .
.
![]() be between
be between ![]() and
and ![]() , inclusive. We know that
, inclusive. We know that
![]() , since this is a property in the definition of
, since this is a property in the definition of ![]() .
So, since
.
So, since ![]() , by Theorem 37,
, by Theorem 37,
![]() , which is what we wanted to show.
, which is what we wanted to show.
![]() between
between ![]() and
and ![]() , inclusive,
it follows that
, inclusive,
it follows that
![]() and
and ![]() , then
, then ![]() .
.
![]() be between
be between ![]() and
and ![]() , inclusive. Since
, inclusive. Since ![]() , by Theorem
37,
, by Theorem
37,
![]() . So, this is true for all
. So, this is true for all ![]() between
between ![]() and
and ![]() , so
by the definition of
, so
by the definition of ![]() , it follows that
, it follows that ![]() , which is what we wanted to show.
, which is what we wanted to show.