



Next: k-Fibonacci-q numbers and new
Up: Fibonacci-q numbers and new
Previous: Definitions
Contents
Done by strong mathematical induction on 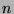 .
.
Base Case:  and
and  . WTS:
. WTS:
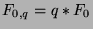 and
and
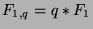 .
.
Since
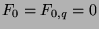 and
and 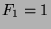 and
and  , both of these are true.
, both of these are true.
Induction Step: Assume
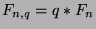 and
and
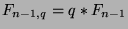 .
.
WTS:
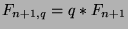 .
.
We can add the two equations that we know together to get
 , or
, or
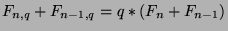 . Since
. Since
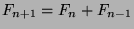 and
and
 , we can substitute to get
, we can substitute to get
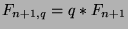 , which is what we wanted to show.
, which is what we wanted to show.
We will prove this by showing that 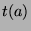 satisfies the definition of
satisfies the definition of 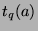 .
.
Part 1: WTS:  .
.
This is a property included in the definition of 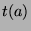 .
.
Part 2: WTS:
 .
.
By the definition of 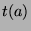 ,
,
 . Thus, by Theorem
28,
. Thus, by Theorem
28,
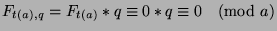 , which is what we
wanted to show.
, which is what we
wanted to show.
Part 3: WTS:
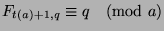 .
.
By the definition of 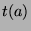 ,
,
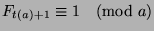 . Thus, by Theorem
28,
. Thus, by Theorem
28,
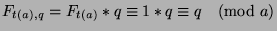 , which is what we
wanted to show.
, which is what we
wanted to show.
Part 4: WTS: If 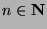 and
and 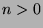 and
and
 and
and
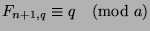 , then
, then 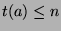 .
.
First, note that since 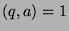 , then by Fact 5, there exists integers
, then by Fact 5, there exists integers
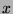 and
and  such that
such that 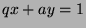 , so
, so  , so
, so
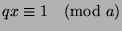 (by the definition
of mod). Now, by Theorem 28,
(by the definition
of mod). Now, by Theorem 28,
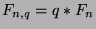 , so, multiplying both sides by
, so, multiplying both sides by
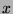 , we find that
, we find that
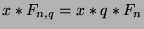 , or
, or
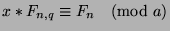 . Similarly,
. Similarly,
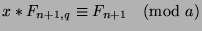 . Now, since
. Now, since
 , then
, then
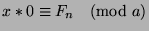 , or
, or
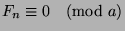 . Similarly, since
. Similarly, since
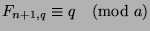 , then
, then
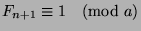 . Now, by Theorem
9,
. Now, by Theorem
9,  , so by Fact 3,
, so by Fact 3, 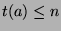 , which is what we wanted to show.
, which is what we wanted to show.
Part 1: WTS: If 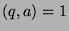 and
and
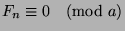 , then
, then
 .
.
By Theorem 28,
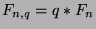 , so
, so
 . Since
. Since
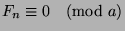 , then
, then
 , or
, or
 , which is what we wanted
to show.
, which is what we wanted
to show.
Part 2: WTS: If 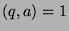 and
and
 , then
, then
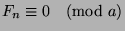 .
.
By Theorem 28,
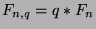 , so
, so
 . Since
. Since
 , then
, then
 . Since
. Since 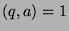 , by Fact 14
, by Fact 14
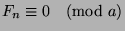 , which is what we wanted to show.
, which is what we wanted to show.
We will prove this by showing that  satisfies the properties of
satisfies the properties of  .
.
Part 1: WTS: 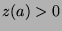 .
.
This is a property in the definition of  .
.
Part 2: WTS:
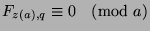 .
.
We know that
 , since this is a property in
the definition of
, since this is a property in
the definition of  . So, since
. So, since 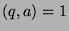 , by Theorem 30,
, by Theorem 30,
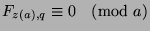 , which is what we wanted to show.
, which is what we wanted to show.
Part 3: WTS: If
 and
and 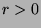 , then
, then 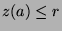 .
.
Since 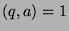 , by Theorem 30,
, by Theorem 30,
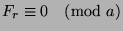 .
So, by the definition of
.
So, by the definition of  ,
, 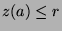 , which is what we wanted to show.
, which is what we wanted to show.
First, note that
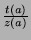 exists by Theorem 12. Now, since
exists by Theorem 12. Now, since
 , then
, then 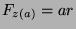 for some
for some 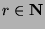 . Now, let
. Now, let
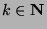 . By Theorem 2,
. By Theorem 2,
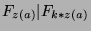 , or
, or 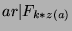 . So,
. So,
 , and by Fact 16,
, and by Fact 16,
 .
Thus, every position in the Fibonacci sequence of the form
.
Thus, every position in the Fibonacci sequence of the form 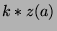 is congruent to
is congruent to
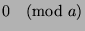 . Also, by Theorem 5, if
. Also, by Theorem 5, if
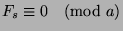 , where
, where 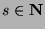 ,
then
,
then  , which means that
, which means that 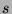 can be represented in the form
can be represented in the form 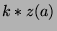 . Thus, these
positions in the Fibonacci sequence are the only ones that are congruent to
. Thus, these
positions in the Fibonacci sequence are the only ones that are congruent to 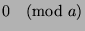 . So,
now we must count the number between
. So,
now we must count the number between 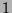 and
and 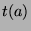 . Since they occur every
. Since they occur every  places,
and since
places,
and since 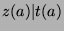 (by Theorem 12), we conclude that there are
(by Theorem 12), we conclude that there are
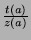 such places in the Fibonacci sequence between
such places in the Fibonacci sequence between 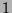 and
and 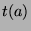 . Thus,
. Thus,
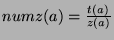 .
.
Note that this implies that
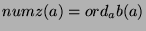 by Theorem 13.
by Theorem 13.
By Theorem 29,
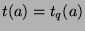 . By Theorem 30, the positions
of the zeros in the Fibonacci sequence and the Fibonacci-
. By Theorem 30, the positions
of the zeros in the Fibonacci sequence and the Fibonacci-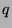 sequence are exactly the same,
so by the definition of
sequence are exactly the same,
so by the definition of 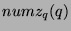 , it follows that
, it follows that
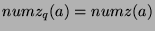 .
.
This will be proven by a construction. First, write down all Fibonacci-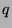 sequences from the 1st term to the
sequences from the 1st term to the 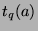 term modulo
term modulo 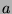 such that
such that 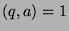 and
and
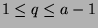 . Note that the
number of such sequences is just
. Note that the
number of such sequences is just 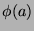 . Now, by Theorem 29, each of these
sequences is the same length, and by Theorem 30, all terms of value
. Now, by Theorem 29, each of these
sequences is the same length, and by Theorem 30, all terms of value 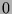 will be at
the same position in every sequence. Now, consider terms whose position is of the form
will be at
the same position in every sequence. Now, consider terms whose position is of the form
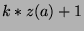 , where
, where 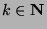 or
or 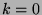 . These terms will be denoted by "
. These terms will be denoted by " terms". By
Theorem
31, these will all be after the only
terms". By
Theorem
31, these will all be after the only 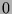 s in their sequences, and by Theorem 33,
there will be the same number of them in each sequence. Now, we start with the first sequence
and look at all
s in their sequences, and by Theorem 33,
there will be the same number of them in each sequence. Now, we start with the first sequence
and look at all  terms in that sequence. Then, we will search for a sequence in which any
terms in that sequence. Then, we will search for a sequence in which any
 term is equal to any
term is equal to any  term in the first sequence. Now, assume there is a
term in the first sequence. Now, assume there is a  term in the
term in the 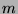 th line that is equal to some
th line that is equal to some  term in the
term in the 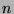 th line. Since all Fibonacci-
th line. Since all Fibonacci-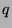 sequences are determined by 2 consecutive terms (like the Fibonacci sequence),
and all
sequences are determined by 2 consecutive terms (like the Fibonacci sequence),
and all  terms are preceded by a
terms are preceded by a 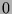 , we can say
that these two sequences are in fact the same sequence shifted by
, we can say
that these two sequences are in fact the same sequence shifted by 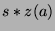 terms, where
terms, where 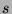 is
some integer. So, all
is
some integer. So, all  terms in the 2 sequences will be the same. Therefore, we can
eliminate or cross out one of these sequences, while still keeping all numbers that were
terms in the 2 sequences will be the same. Therefore, we can
eliminate or cross out one of these sequences, while still keeping all numbers that were  terms. Continue this until there are no more duplicate
terms. Continue this until there are no more duplicate  terms left. Now, we will show that
all
terms left. Now, we will show that
all  terms in all Fibonacci-
terms in all Fibonacci-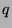 sequences (where
sequences (where 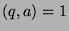 )
are relatively prime to
)
are relatively prime to 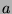 . First, looking back at the proof of Theorem 13, we
established that
. First, looking back at the proof of Theorem 13, we
established that
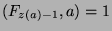 . Since
. Since
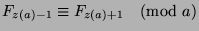 , we can
say that
, we can
say that
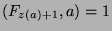 . Now, Theorem 7 states that if
. Now, Theorem 7 states that if
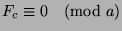 , then
, then
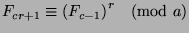 . We can plug in
. We can plug in
 for
for 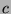 in this formula and notice that
in this formula and notice that
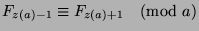 to say that
to say that
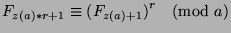 . Now, since we know that
. Now, since we know that
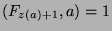 ,
by Fact 12 we can say that
,
by Fact 12 we can say that
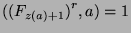 for all
for all 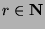 . We can reduce this to say that
. We can reduce this to say that
 for all
for all 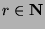 , which says that every
, which says that every  term
in the Fibonacci sequence is relatively prime to
term
in the Fibonacci sequence is relatively prime to 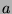 . Now, since we are considering every
Fibonacci-
. Now, since we are considering every
Fibonacci-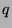 sequence such that
sequence such that 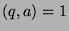 , by Fact 11 we can say that
, by Fact 11 we can say that
 . By Theorem 28, these are just the
. By Theorem 28, these are just the  terms in all of the
Fibonacci-
terms in all of the
Fibonacci-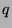 sequences, so all
sequences, so all  in every sequence listed are relatively prime to
in every sequence listed are relatively prime to 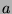 .
Notice that every sequence starts with a
.
Notice that every sequence starts with a  term, and since the first term of every
Fibonacci-
term, and since the first term of every
Fibonacci-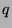 sequence is just
sequence is just 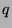 , we have started with all relatively prime numbers less than
, we have started with all relatively prime numbers less than
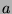 . Every time we eliminate a sequence, there is still at least 1 copy left of every number
relatively prime to
. Every time we eliminate a sequence, there is still at least 1 copy left of every number
relatively prime to 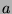 and less than
and less than 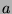 , since there are 2 copies of the same
, since there are 2 copies of the same  term in
each sequence, and only 1 is removed. If there is more than 1 copy left, we eliminate one of
the sequences, so after we are finished there is exactly 1 and only 1 copy of every number
less than
term in
each sequence, and only 1 is removed. If there is more than 1 copy left, we eliminate one of
the sequences, so after we are finished there is exactly 1 and only 1 copy of every number
less than 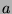 and relatively prime to
and relatively prime to 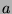 . Now, we will count the number of
. Now, we will count the number of  terms left in 2
different ways. By
the definition of
terms left in 2
different ways. By
the definition of 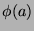 , there are exactly
, there are exactly 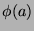
 terms left. Also, since every
terms left. Also, since every 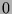 in each sequence corresponds to a
in each sequence corresponds to a  term (the
term (the 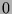 in the
in the 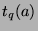 position corresponds to
the
position corresponds to
the  term in the first position), and there are
term in the first position), and there are 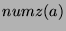
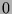 s in every sequence, we can say
that there are
s in every sequence, we can say
that there are 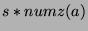
 terms, where
terms, where 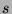 is the number of sequences left. So,
is the number of sequences left. So,
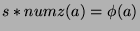 , or
, or
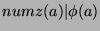 by the definition of divides.
by the definition of divides.




Next: k-Fibonacci-q numbers and new
Up: Fibonacci-q numbers and new
Previous: Definitions
Contents
Gregory Stoll
2000-04-08
![]() and
and ![]() . WTS:
. WTS:
![]() and
and
![]() .
.
![]() and
and ![]() and
and ![]() , both of these are true.
, both of these are true.
![]() and
and
![]() .
.
![]() .
.
![]() , or
, or
![]() . Since
. Since
![]() and
and
![]() , we can substitute to get
, we can substitute to get
![]() , which is what we wanted to show.
, which is what we wanted to show.
![]() .
.
![]() .
.
![]() .
.
![]() ,
,
![]() . Thus, by Theorem
28,
. Thus, by Theorem
28,
![]() , which is what we
wanted to show.
, which is what we
wanted to show.
![]() .
.
![]() ,
,
![]() . Thus, by Theorem
28,
. Thus, by Theorem
28,
![]() , which is what we
wanted to show.
, which is what we
wanted to show.
![]() and
and ![]() and
and
![]() and
and
![]() , then
, then ![]() .
.
![]() , then by Fact 5, there exists integers
, then by Fact 5, there exists integers
![]() and
and ![]() such that
such that ![]() , so
, so ![]() , so
, so
![]() (by the definition
of mod). Now, by Theorem 28,
(by the definition
of mod). Now, by Theorem 28,
![]() , so, multiplying both sides by
, so, multiplying both sides by
![]() , we find that
, we find that
![]() , or
, or
![]() . Similarly,
. Similarly,
![]() . Now, since
. Now, since
![]() , then
, then
![]() , or
, or
![]() . Similarly, since
. Similarly, since
![]() , then
, then
![]() . Now, by Theorem
9,
. Now, by Theorem
9, ![]() , so by Fact 3,
, so by Fact 3, ![]() , which is what we wanted to show.
, which is what we wanted to show.
![]() and
and
![]() , then
, then
![]() .
.
![]() , so
, so
![]() . Since
. Since
![]() , then
, then
![]() , or
, or
![]() , which is what we wanted
to show.
, which is what we wanted
to show.
![]() and
and
![]() , then
, then
![]() .
.
![]() , so
, so
![]() . Since
. Since
![]() , then
, then
![]() . Since
. Since ![]() , by Fact 14
, by Fact 14
![]() , which is what we wanted to show.
, which is what we wanted to show.
![]() .
.
![]() .
.
![]() .
.
![]() , since this is a property in
the definition of
, since this is a property in
the definition of ![]() . So, since
. So, since ![]() , by Theorem 30,
, by Theorem 30,
![]() , which is what we wanted to show.
, which is what we wanted to show.
![]() and
and ![]() , then
, then ![]() .
.
![]() , by Theorem 30,
, by Theorem 30,
![]() .
So, by the definition of
.
So, by the definition of ![]() ,
, ![]() , which is what we wanted to show.
, which is what we wanted to show.
![]() by Theorem 13.
by Theorem 13.