



Next: About this document ...
Up: Generalized a,b-Fibonacci numbers (this
Previous: Definitions
Contents
Crucial Note: In this section, we will only consider
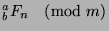 such that
such that
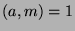 and
and
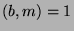 - otherwise,
- otherwise, 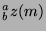 and
and 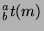 are not guaranteed to exist.
are not guaranteed to exist.
Theorem 41
The generalized 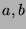 -Fibonacci numbers are periodic in any modulo.
-Fibonacci numbers are periodic in any modulo.
Consider the generalized 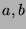 -Fibonacci sequence in mod
-Fibonacci sequence in mod 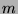 :
:
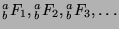 . Now,
consider the pairs of consecutive generalized
. Now,
consider the pairs of consecutive generalized 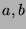 -Fibonacci numbers (for
example
-Fibonacci numbers (for
example
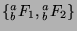 ,
,
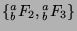 , etc.). Since
we are in mod
, etc.). Since
we are in mod 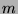 , there are only
, there are only
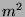 possible distinct such pairs (since there are
possible distinct such pairs (since there are 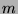 choices for the first
number in a pair and
choices for the first
number in a pair and 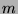 choices for the second number in a pair). If
choices for the second number in a pair). If 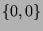 is
one such pair, then the whole sequence must be
is
one such pair, then the whole sequence must be
 in mod
in mod 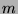 ,
which contradicts the initial conditions of the sequence, so there are only
,
which contradicts the initial conditions of the sequence, so there are only
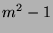 possible distinct pairs. Since the Fibonacci sequence is infinite,
there are an infinite number of pairs, so by the Pigeonhole Principle, at least
one of these pairs must repeat. Suppose that the pairs
possible distinct pairs. Since the Fibonacci sequence is infinite,
there are an infinite number of pairs, so by the Pigeonhole Principle, at least
one of these pairs must repeat. Suppose that the pairs
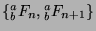 and
and
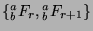 are the same (that is,
are the same (that is,
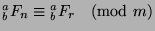 and
and
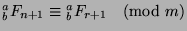 ). WLOG
(without loss of generality), let
). WLOG
(without loss of generality), let
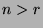 . Then, we know that
. Then, we know that
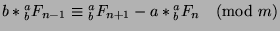 (and since
(and since 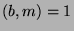 ,
,
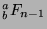 has a unique solution) and
has a unique solution) and
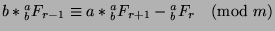 (and since
(and since 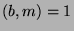 ,
,
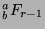 has a unique solution), so
has a unique solution), so
 .
We can continue this until we find that
.
We can continue this until we find that
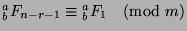 and
and
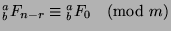 , so
, so 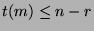 . So, we can continue
this in the other direction and find that the generalized
. So, we can continue
this in the other direction and find that the generalized  -Fibonacci sequence is periodic.
-Fibonacci sequence is periodic.
Done by strong mathematical induction on 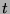 .
.
Base Case:  . WTS:
. WTS:
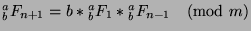 .
.
By the definition of the Fibonacci sequence,
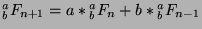 ,
so
,
so
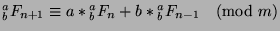 . Since
. Since
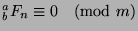 , then
, then
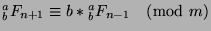 . Since
. Since
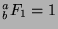 , we can multiply to get that
, we can multiply to get that
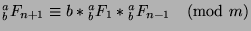 ,
which is what we wanted to show.
,
which is what we wanted to show.
Induction Step: Assume
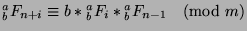 ,
,
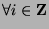 such that
such that 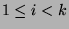 .
.
WTS:
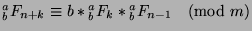 .
.
Since 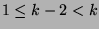 and
and 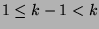 , we can say that
, we can say that
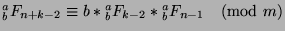 and
and
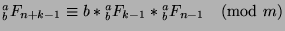 . We
can multiply the first by
. We
can multiply the first by 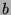 and the second by
and the second by 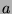 to say that
to say that
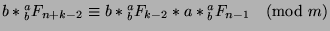 and
and
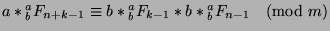 . We
can add these equations together to say that
. We
can add these equations together to say that
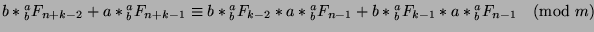 . Factoring,
we get that
. Factoring,
we get that
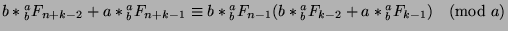 . Since
. Since
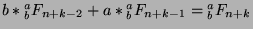 and
and
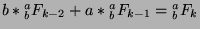 , we can substitute to say that
, we can substitute to say that
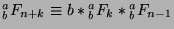 , which is what we wanted to show.
, which is what we wanted to show.
Let 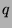 be the integer such that
be the integer such that
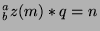 (this is guaranteed to exist by
the definition of divides). Now we will use weak mathematical induction on
(this is guaranteed to exist by
the definition of divides). Now we will use weak mathematical induction on 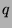 .
.
Base Case: 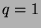 . WTS:
. WTS:
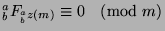 .
.
This follows from the definition of 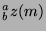 .
.
Induction Step: Assume
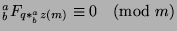 .
.
WTS:
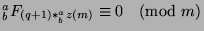 .
.
Since
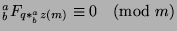 (given), we can apply
Theorem 42 to say that
(given), we can apply
Theorem 42 to say that
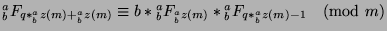 . Since
. Since
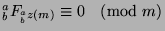 (by the definition of
(by the definition of  , we can say that
, we can say that
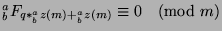 . Simplifying, we get that
. Simplifying, we get that
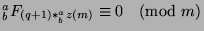 , which is what we wanted to show.
, which is what we wanted to show.
Let 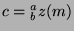 . Divide
. Divide 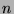 by
by 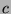 to get
to get 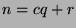 , where
, where
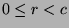 . So,
. So,
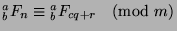 . Since
. Since
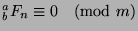 ,
then
,
then
 . By Theorem 43,
. By Theorem 43,
 . So we can apply Theorem 42
to say that
. So we can apply Theorem 42
to say that
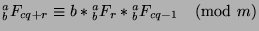 . Now, since
. Now, since
 , we can say that
, we can say that
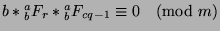 . Since
. Since 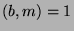 , by Fact
14 we know that
, by Fact
14 we know that
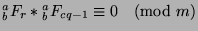 . Now,
assume for the sake of contradiction that
. Now,
assume for the sake of contradiction that
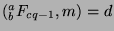 , where
, where 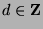 and
and
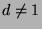 . So,
. So, 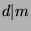 and
and
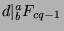 . Now, since
. Now, since
 (by Theorem 43), then
(by Theorem 43), then
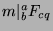 , and since
, and since 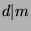 , then
, then
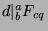 . Now, we notice that
. Now, we notice that 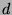 divides 2 consecutive terms of the generalized
divides 2 consecutive terms of the generalized 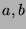 -Fibonacci sequence, and since this
sequence is determined by 2 consecutive terms, all terms past these 2 in the sequence
must be divisible by
-Fibonacci sequence, and since this
sequence is determined by 2 consecutive terms, all terms past these 2 in the sequence
must be divisible by 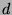 . Now, consider the
. Now, consider the 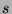 th term, where
th term, where 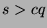 . So, by the
previous argument,
. So, by the
previous argument, 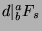 . So,
. So,
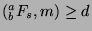 , since
, since 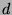 is a common
factor, and since
is a common
factor, and since 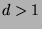 , then
, then
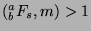 , or
, or
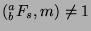 . Now, we can
take the contrapositive of Fact 6 to say that if
. Now, we can
take the contrapositive of Fact 6 to say that if
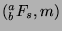 does not divide
does not divide
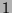 , then there do not exist integers
, then there do not exist integers 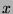 and
and 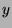 such that
such that
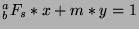 , so we
know that there do not exist integers
, so we
know that there do not exist integers 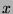 and
and 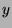 such that
such that
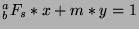 , so
, so
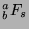 is not congruent to
is not congruent to  . Now we have shown this for all
. Now we have shown this for all 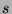 such that
such that
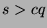 - but
this is a contradiction to the fact that the generalized
- but
this is a contradiction to the fact that the generalized 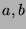 -Fibonacci sequence is periodic!
So, we reject our hypothesis, and conclude that
-Fibonacci sequence is periodic!
So, we reject our hypothesis, and conclude that
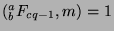 . Then, by Fact
14,
. Then, by Fact
14,
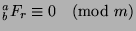 . Now, we know that
. Now, we know that 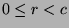 . If
. If 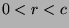 ,
then we have a contradiction to the definition of
,
then we have a contradiction to the definition of 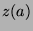 (since
(since 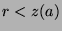 , but satisfies the definition
of
, but satisfies the definition
of 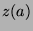 ). Thus, we reject that case, and conclude that
). Thus, we reject that case, and conclude that  . Thus,
. Thus, 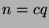 , which means that
, which means that
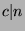 , or
, or 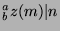 .
.
Done by weak mathematical induction on 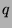 .
.
Base Case: 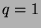 . WTS:
. WTS:
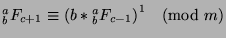 .
.
Since
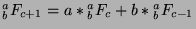 , then
since
, then
since
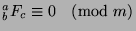 , we know that
, we know that
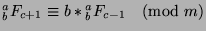 , or
, or
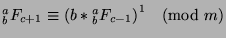 ,
which is what we wanted to show.
,
which is what we wanted to show.
Induction Step: Assume
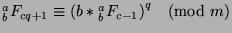 .
.
WTS:
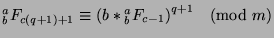 .
.
Note that
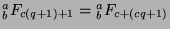 . Now, since
. Now, since
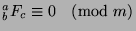 , we know by Theorem 42 that
, we know by Theorem 42 that
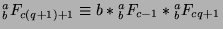 . Now, by the
given,
. Now, by the
given,
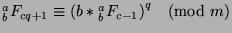 , so we can
substitute to get
, so we can
substitute to get
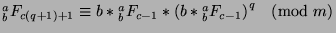 . We
can simplify this to say that
. We
can simplify this to say that
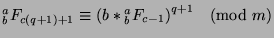 , which is what we
wanted to show.
, which is what we
wanted to show.
Since
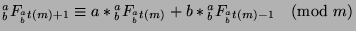 ,
then
,
then
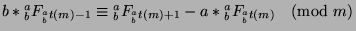 .
If we let
.
If we let 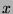 be an integer such that
be an integer such that
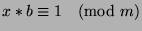 (
(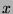 exists by the fact that
exists by the fact that
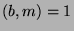 and Fact 13), then we can say that
and Fact 13), then we can say that
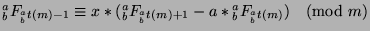 .
Since
.
Since
 (by definition of
(by definition of 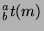 we can simplify
this to
we can simplify
this to
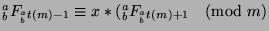 . We know that
. We know that
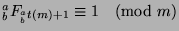 by the definition of
by the definition of 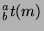 , so we can
substitute to say that
, so we can
substitute to say that
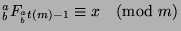 . Now, by Theorem
45,
. Now, by Theorem
45,
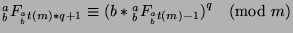 (since
(since
 ), which means that
), which means that
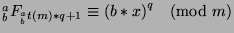 , or
, or
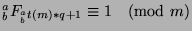 . Now, we can work backwards using the
ideas from the preceding steps to determine that
. Now, we can work backwards using the
ideas from the preceding steps to determine that
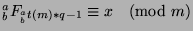 . Also,
. Also,
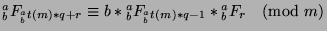 by Theorem 42. So, we can substitute to say that
by Theorem 42. So, we can substitute to say that
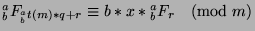 , and since we defined
, and since we defined 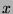 such that
such that
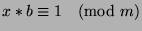 , we conclude that
, we conclude that
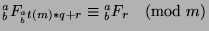 , which is what we wanted to show.
, which is what we wanted to show.
Let 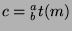 . Divide
. Divide 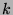 by
by 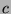 to get
to get 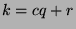 , where
, where 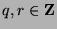 and
and
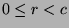 . Since
. Since
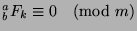 , then
, then
 ,
so
,
so
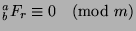 (by Theorem 46). Since
(by Theorem 46). Since
 , then
, then
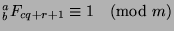 ,
so
,
so
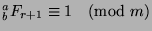 (by Theorem 46). If
(by Theorem 46). If
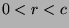 , then
, then 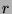 satisfies the definition of
satisfies the definition of 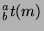 ,
but is smaller than
,
but is smaller than 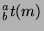 (since
(since 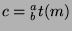 ), which is a contradiction. So,
), which is a contradiction. So,
 , and
, and 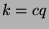 , so
, so 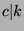 , and
, and 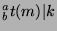 , which is what we wanted to show.
, which is what we wanted to show.
 and
and
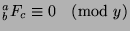 , so
, so
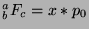 and
and
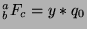 for some
for some
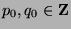 . So,
. So, 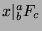 and
and 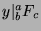 , and since
, and since 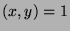 , then
, then
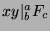 (by Fact
8). So,
(by Fact
8). So,
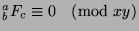 . Now, since
. Now, since
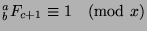 and
and
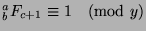 ,
then
,
then
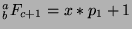 and
and
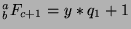 for some
for some
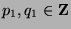 . So,
. So,
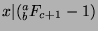 and
and
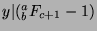 ,
and since
,
and since 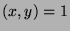 , then
, then
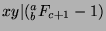 (by Fact 8). So,
(by Fact 8). So,
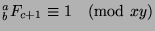 . By Theorem 47,
. By Theorem 47,
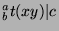 ,
which is what we wanted to show.
,
which is what we wanted to show.
![${^a _b}t(x)\vert[{^a _b}t(x),{^a _b}t(y)]$](img995.png) and
and
![${^a _b}t(x)\vert[{^a _b}t(x),{^a _b}t(y)]$](img995.png) (by definition of LCM), and since
(by definition of LCM), and since 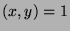 ,
then
,
then
![${^a _b}t(xy)\vert[{^a _b}t(x),{^a _b}t(y)]$](img996.png) (by Theorem 48).
(by Theorem 48).
 and
and
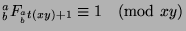 , so
, so
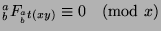 and
and
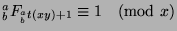 by Fact 16, so by Theorem
47,
by Fact 16, so by Theorem
47,
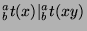 . Since
. Since
 and
and
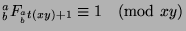 , so
, so
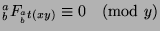 and
and
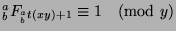 by Fact 16, so
by Theorem 47,
by Fact 16, so
by Theorem 47,
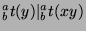 . So,
by definition of LCM,
. So,
by definition of LCM,
![$[{^a _b}t(x),{^a _b}t(y)]\vert{^a _b}t(xy)$](img1005.png) . Since
. Since
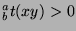 and
and
![$[{^a _b}t(x),{^a _b}t(y)]>0$](img1007.png) , by Fact 15
, by Fact 15
![${^a _b}t(xy)=[{^a _b}t(x),{^a _b}t(y)]$](img1008.png) .
.




Next: About this document ...
Up: Generalized a,b-Fibonacci numbers (this
Previous: Definitions
Contents
Gregory Stoll
2000-04-08
![]() . WTS:
. WTS:
![]() .
.
![]() ,
so
,
so
![]() . Since
. Since
![]() , then
, then
![]() . Since
. Since
![]() , we can multiply to get that
, we can multiply to get that
![]() ,
which is what we wanted to show.
,
which is what we wanted to show.
![]() ,
,
![]() such that
such that ![]() .
.
![]() .
.
![]() and
and ![]() , we can say that
, we can say that
![]() and
and
![]() . We
can multiply the first by
. We
can multiply the first by ![]() and the second by
and the second by ![]() to say that
to say that
![]() and
and
![]() . We
can add these equations together to say that
. We
can add these equations together to say that
![]() . Factoring,
we get that
. Factoring,
we get that
![]() . Since
. Since
![]() and
and
![]() , we can substitute to say that
, we can substitute to say that
![]() , which is what we wanted to show.
, which is what we wanted to show.
![]() . WTS:
. WTS:
![]() .
.
![]() .
.
![]() .
.
![]() .
.
![]() (given), we can apply
Theorem 42 to say that
(given), we can apply
Theorem 42 to say that
![]() . Since
. Since
![]() (by the definition of
(by the definition of ![]() , we can say that
, we can say that
![]() . Simplifying, we get that
. Simplifying, we get that
![]() , which is what we wanted to show.
, which is what we wanted to show.
![]() . WTS:
. WTS:
![]() .
.
![]() , then
since
, then
since
![]() , we know that
, we know that
![]() , or
, or
![]() ,
which is what we wanted to show.
,
which is what we wanted to show.
![]() .
.
![]() .
.
![]() . Now, since
. Now, since
![]() , we know by Theorem 42 that
, we know by Theorem 42 that
![]() . Now, by the
given,
. Now, by the
given,
![]() , so we can
substitute to get
, so we can
substitute to get
![]() . We
can simplify this to say that
. We
can simplify this to say that
![]() , which is what we
wanted to show.
, which is what we
wanted to show.