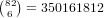 .
. Point values in the game “Target”
Target is a game where you draw cards to try to satisfy the target cards. Each of the cards has a separate point value, and I wondered how ”true” those points were. So, my goal was to calculate the number of 6 card hands (in the game your hand limit is 5, but you draw a card and then can turn sets in) that satisfy each of the conditions and see if there was a way to derive how points were allocated. It was also a good excuse to calculate (using combinatorics) the exact number of hands that satisfy each condition, and to check those numbers using a Python script.
Target cards are 0-9 in four different suits (purple, green, red, blue) plus 1 wild suit
in each number. 0 and 9 have one of each suit and all other numbers have two of each
suit for a total of 2(4 + 1) + 8(2 ⋅ 4 + 1) = 82 cards. The total number of possible
hands is 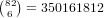 .
.
The x-axis represents the probability that a random 6-card hand will satisfy the
target card. The y-axis is just the number of cards you have to turn in to fulfill the
target card, and the color of the dot (and the corresponding text) is how many points
it’s worth. So, dots in the upper-left hand corner are the hardest to get and take the
most cards, and you would expect these to be worth the most points (which they
generally are).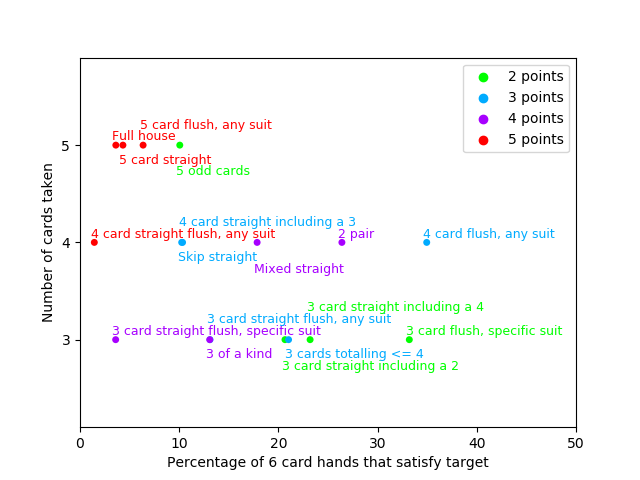
There are some interesting results here - all the 5 point targets are at the left and
towards the top, as expected, but there are some interesting outliers. At 2 points,
5 odd cards seems undervalued; it’s the only target that takes more than
3 cards that’s only worth 2 points (and it has a pretty low probability to
boot). 4 card straight including a 3 and skip straight both seem undervalued
since mixed straight is more likely and is worth more points. 3 card straight
including a 2 looks similarly undervalued. (or maybe 3 cards totalling ¡= 4 is
overvalued?)
One possibility is that the designers of the game looked at the probabilities with 5 card hands instead of 6 cards as I’ve done. Another is that they chose to fiddle with the point values to account for the fact that certain target cards are easier to turn in together - if you have 5 odd cards you have a pretty good chance of having a skip straight, etc.
I was able to calculate almost all the results symbolically. Here are the results.
Click on a hand type to see the derivation of that number. These results
were derived by hand (except the ones in bold) and checked with a Python
script.
| Hand type | Points | Possible hands | Probability | |
| Flush | ||||
| 3 card, specific suit | 2 | 116241489 | 33.197% | |
| 4 card, any suit | 3 | 122384088 | 34.951% | |
| 5 card, any suit | 5 | 22272138 | 6.361% | |
| Straight | ||||
| 3 card including a 2 | 2 | 72355734 | 20.664% | |
| 3 card including a 4 | 2 | 81222993 | 23.196% | |
| 3 card including a 5 | 2 | 81222993 | 23.196% | |
| 3 card including a 7 | 2 | 72355734 | 20.664% | |
| 4 card including a 3 | 3 | 36204327 | 10.339% | |
| 4 card including a 6 | 3 | 36204327 | 10.339% | |
| 5 card | 5 | 15149349 | 4.326% | |
| Straight Flush | ||||
| 3 card, specific suit | 4 | 12588978 | 3.595% | |
| 3 card, any suit | 3 | 45888079 | 13.105% | |
| 4 card, any suit | 5 | 5054955 | 1.444% | |
| Poker | ||||
| 2 pair | 4 | 92445176 | 26.401% | |
| 3 of a kind | 4 | 45800298 | 13.080% | |
| Full house | 5 | 12646280 | 3.612% | |
| Misc | ||||
| 5 odd cards | 2 | 35221706 | 10.059% | |
| 5 even cards | 2 | 35221706 | 10.059% | |
| 3 cards totalling ≤ 4 | 3 | 73617980 | 21.024% | |
| 3 cards totalling ≥ 23 | 3 | 73617980 | 21.024% | |
| Skip straight | 3 | 35894502 | 10.251% | |
| Mixed straight | 4 | 62519949 | 17.855% | |
Without loss of generality, let the suit be G(reen). There are 28 cards that can be G - 18 G and 10 W(ild), and so there are 82 - 28 = 54 cards that cannot be G. To avoid double-counting, we split up the possibilities:


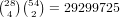
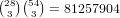
So the total is 376740 + 5307120 + 29299725 + 81257904 = 116241489.
Back to table
We break it down by the number of wilds in the hand. Note that there are 10 wilds and 18 cards of each suit, which means there are 54 cards not in a given suit.
 possibilities, which gives
possibilities, which gives
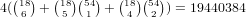 .
.
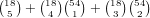 choices for the cards in that suit, which
gives
choices for the cards in that suit, which
gives 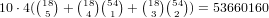 .
.
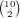 choices for which wilds we have. There are 4
cards left and we only need 2 of the same suit to make a flush, so only 1
card in each suit will fail to give a flush. There are 184 failures, so there
are
choices for which wilds we have. There are 4
cards left and we only need 2 of the same suit to make a flush, so only 1
card in each suit will fail to give a flush. There are 184 failures, so there
are 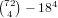 possibilities, which gives
possibilities, which gives 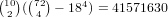 .
.
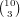 choices for which wilds we have, and any
remaining set of cards will give a 4 card flush, so there are
choices for which wilds we have, and any
remaining set of cards will give a 4 card flush, so there are 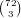 possibilities, which gives
possibilities, which gives 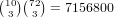 .
.
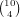 choices for which wilds we have, and any
remaining set of cards will give a 4 card flush, so there are a total of
choices for which wilds we have, and any
remaining set of cards will give a 4 card flush, so there are a total of
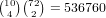 possibilities.
possibilities.
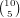 choices for which wilds we have, and any
remaining set of cards will give a 4 card flush, so there are a total of
choices for which wilds we have, and any
remaining set of cards will give a 4 card flush, so there are a total of
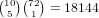 possibilities.
possibilities.
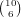 possibilities.
possibilities.So, the total is 19440384+53660160+41571630+7156800+536760+18144+210 = 122384088.
Back to table
Similarly, we break it down by the number of wilds in the hand.
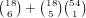 possibilities, which gives
possibilities, which gives
 .
.
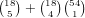 possibilities for those cards, which
gives a total of
possibilities for those cards, which
gives a total of 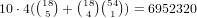 .
.
 choices for which wilds we have. We need 3
cards in any one suit to give a flush and there are 4 cards left so there
is no danger of overcounting. Thus, there are 4 choices for a suit and
choices for which wilds we have. We need 3
cards in any one suit to give a flush and there are 4 cards left so there
is no danger of overcounting. Thus, there are 4 choices for a suit and
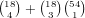 choices for the cards in that suit, which gives a total of
choices for the cards in that suit, which gives a total of
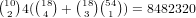 .
.
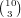 choices for which wilds we have. We need 2
cards in any one suit to give a flush and there are 3 cards left so there
is no danger of overcounting. Thus, there are 4 choices for a suit and
choices for which wilds we have. We need 2
cards in any one suit to give a flush and there are 3 cards left so there
is no danger of overcounting. Thus, there are 4 choices for a suit and
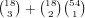 choices for the cards in that suit, which gives a total of
choices for the cards in that suit, which gives a total of
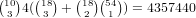 .
.
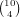 choices for which wilds we have, and any
remaining cards will give a flush, so there are a total of
choices for which wilds we have, and any
remaining cards will give a flush, so there are a total of 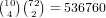 possibilities.
possibilities.
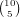 choices for which wilds we have, and any
remaining set of cards will give a flush, so there are a total of
choices for which wilds we have, and any
remaining set of cards will give a flush, so there are a total of
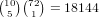 possibilities.
possibilities.
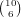 possibilities.
possibilities.So, the total is 1924944+6952320+8482320+4357440+536760+18144+210 = 22272138.
Back to table
We break it down by the length of the straight:
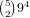 of these,
and if anywhere from 1-4 has 2 cards there are
of these,
and if anywhere from 1-4 has 2 cards there are  . So for a 0-4
straight there are
. So for a 0-4
straight there are 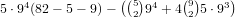 possibilities.
Using a similar technique, for a 1-5 straight there are 95(82 - 5 - 5 -
9) possibilities, but we overcounted the (2,1,1,1,1) distributions so the
true number is
possibilities.
Using a similar technique, for a 1-5 straight there are 95(82 - 5 - 5 -
9) possibilities, but we overcounted the (2,1,1,1,1) distributions so the
true number is 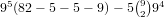 , and for a 2-6 straight there
are 95(82 - 5 - 9 - 9) possibilities, but we overcounted the (2,1,1,1,1)
distributions so the true number is
, and for a 2-6 straight there
are 95(82 - 5 - 9 - 9) possibilities, but we overcounted the (2,1,1,1,1)
distributions so the true number is 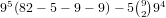 . This
gives us a total of
. This
gives us a total of 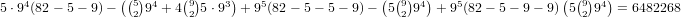 .
.
 .
For the 1-4 case our universe is all cards except any 0 or 5, so there are 82-
5-9 = 68 cards in our universe. We get
.
For the 1-4 case our universe is all cards except any 0 or 5, so there are 82-
5-9 = 68 cards in our universe. We get  .
For the 2-5 case our universe is all cards except any 1 or 6, so there are 82-
9-9 = 64 cards in our universe, and we get
.
For the 2-5 case our universe is all cards except any 1 or 6, so there are 82-
9-9 = 64 cards in our universe, and we get 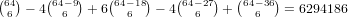 ,
for a total of 5452920 + 7488828 + 6294186 = 19235394.
,
for a total of 5452920 + 7488828 + 6294186 = 19235394.
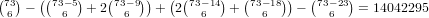 .
For a 1-3 straight our universe is everything except 0’s and 4’s, and there
are 82-5-9 = 68 of these. So we get
.
For a 1-3 straight our universe is everything except 0’s and 4’s, and there
are 82-5-9 = 68 of these. So we get 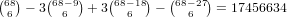 .
For a 2-4 straight our universe is everything except 1’s and 5’s, and there
are 82-9-9 = 64 of these. So we get
.
For a 2-4 straight our universe is everything except 1’s and 5’s, and there
are 82-9-9 = 64 of these. So we get 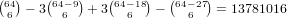 ,
for a total of 14042295 + 17456634 + 13781016 = 45279945.
,
for a total of 14042295 + 17456634 + 13781016 = 45279945.So, the total is 1358127 + 6482268 + 19235394 + 45279945 = 72355734.
Back to table
We break it down by the length of the straight:
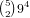 of these,
and if anywhere from 1-4 has 2 cards there are
of these,
and if anywhere from 1-4 has 2 cards there are 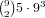 . So for a 0-4
straight there are
. So for a 0-4
straight there are 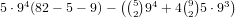 possibilities.
Using a similar technique, for a 1-5 (or 4-8) straight there are 95(82-5-5-
9) possibilities, but we overcounted the (2,1,1,1,1) distributions so the true
number is
possibilities.
Using a similar technique, for a 1-5 (or 4-8) straight there are 95(82-5-5-
9) possibilities, but we overcounted the (2,1,1,1,1) distributions so the true
number is 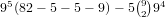 , and for a 2-6 (or 3-7) straight
there are 95(82-5-9-9) possibilities, but we overcounted the (2,1,1,1,1)
distributions so the true number is
, and for a 2-6 (or 3-7) straight
there are 95(82-5-9-9) possibilities, but we overcounted the (2,1,1,1,1)
distributions so the true number is 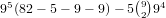 . This
gives us a total of
. This
gives us a total of 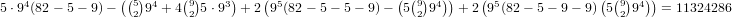 .
.
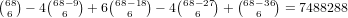 . For
the 2-5 (and 3-6 and 4-7) case our universe is all cards except any 1
or 6, so there are 82 - 9 - 9 = 64 cards in our universe, and we get
. For
the 2-5 (and 3-6 and 4-7) case our universe is all cards except any 1
or 6, so there are 82 - 9 - 9 = 64 cards in our universe, and we get
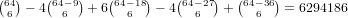 , for a total of
7488828 + 3 ⋅ 6294186 = 26370846.
, for a total of
7488828 + 3 ⋅ 6294186 = 26370846.
 , for a total of 3 ⋅
13781016 = 41343048.
, for a total of 3 ⋅
13781016 = 41343048.So, the total is 2184813 + 11324286 + 26370846 + 41343048 = 81222993.
Back to table
By symmetry this is the same number as 3 card straight including a 4, which is
81222993.
Back to table
By symmetry this is the same number as 3 card straight including a 2, which is
72355734.
Back to table
We break it down into the length of the straight:
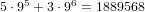 .
.
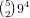 of these, and if anywhere from 1-4 has 2 cards there
are
of these, and if anywhere from 1-4 has 2 cards there
are 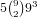 . So for a 0-4 straight there are
. So for a 0-4 straight there are 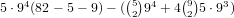 possibilities. Using a similar technique, for a 1-5 straight there are 95(82-
5 - 5 - 9) possibilities, but we overcounted the (2,1,1,1,1) distributions so
the true number is
possibilities. Using a similar technique, for a 1-5 straight there are 95(82-
5 - 5 - 9) possibilities, but we overcounted the (2,1,1,1,1) distributions so
the true number is 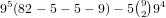 . For a 2-5 straight (and
similarly a 3-6 straight) there are
. For a 2-5 straight (and
similarly a 3-6 straight) there are 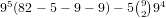 possibilities.
This gives us a total of
possibilities.
This gives us a total of 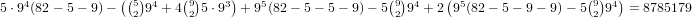 .
.
 possibilities for the other two cards (excluding the cards we already
chose and any 4’s since that would make it a 5 card straight). However,
again we’ve overcounted cases where the extra cards are 0-3. The
distributions of cards we have to exclude are (2,1,1,1), (3,1,1,1), and
(2,2,1,1). For (2,1,1,1), if 0 has 2 cards there are
possibilities for the other two cards (excluding the cards we already
chose and any 4’s since that would make it a 5 card straight). However,
again we’ve overcounted cases where the extra cards are 0-3. The
distributions of cards we have to exclude are (2,1,1,1), (3,1,1,1), and
(2,2,1,1). For (2,1,1,1), if 0 has 2 cards there are  possibilities
and if anywhere from 1-3 has 2 cards there are
possibilities
and if anywhere from 1-3 has 2 cards there are 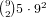 possibilities.
In either case, there are 82 - 5 - 9 ⋅ 4 possibilities for the extra
card, since the extra card can’t be anywhere from 0-4, to avoid
changing the distribution or making it a 5 card straight. For (3,1,1,1),
if 0 has 3 cards there are
possibilities.
In either case, there are 82 - 5 - 9 ⋅ 4 possibilities for the extra
card, since the extra card can’t be anywhere from 0-4, to avoid
changing the distribution or making it a 5 card straight. For (3,1,1,1),
if 0 has 3 cards there are 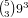 possibilities and otherwise there
are
possibilities and otherwise there
are 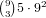 possibilities. For (2,2,1,1), if 0 has 2 cards there are
possibilities. For (2,2,1,1), if 0 has 2 cards there are
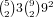 possibilities and otherwise there are
possibilities and otherwise there are  possibilities.
Note that we have to subtract 2 times the number of (3,1,1,1) overcounting
(since we’ve counted these 3⋅1⋅1⋅1 times and we want to only count
them once) and 3 times the number of (2,2,1,1) overcounting. This
gives us a total of
possibilities.
Note that we have to subtract 2 times the number of (3,1,1,1) overcounting
(since we’ve counted these 3⋅1⋅1⋅1 times and we want to only count
them once) and 3 times the number of (2,2,1,1) overcounting. This
gives us a total of 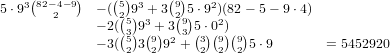
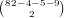 possibilities for the
other cards (excluding the cards we chose and 0’s and 5’s to avoid
5 card straights). For the (2,1,1,1) distribution there are
possibilities for the
other cards (excluding the cards we chose and 0’s and 5’s to avoid
5 card straights). For the (2,1,1,1) distribution there are 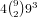 possibilities and 82 - 5 - 9 ⋅ 5 possibilities for the extra card
(avoiding any numbers from 0-5). For the (3,1,1,1) distribution
there are
possibilities and 82 - 5 - 9 ⋅ 5 possibilities for the extra card
(avoiding any numbers from 0-5). For the (3,1,1,1) distribution
there are 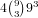 possibilities and for the (2,2,1,1) distribution
there are
possibilities and for the (2,2,1,1) distribution
there are 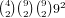 possibilities. This gives us a total of
possibilities. This gives us a total of

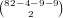 possibilities for the other cards (excluding the cards we chose and
1’s and 6’s to avoid 5 card straights). For the (2,1,1,1) distribution
there are
possibilities for the other cards (excluding the cards we chose and
1’s and 6’s to avoid 5 card straights). For the (2,1,1,1) distribution
there are  possibilities and 82 - 9 ⋅ 6 possibilities for the
extra card (avoiding any numbers from 1-6). For the (3,1,1,1)
distribution there are
possibilities and 82 - 9 ⋅ 6 possibilities for the
extra card (avoiding any numbers from 1-6). For the (3,1,1,1)
distribution there are 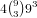 possibilities and for the (2,2,1,1)
distribution there are
possibilities and for the (2,2,1,1)
distribution there are 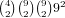 possibilities. This gives us a total
of
possibilities. This gives us a total
of 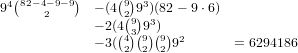
So, the total is 1889568 + 8785179 + 5452920 + 7488288 + 2 ⋅ 6294186 = 36204327.
Back to table
By symmetry this is the same number as 4 card straight including a 3, which is
36204327.
Back to table
We break it down into the length of the straight:
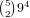 where we have 2 0’s and
where we have 2 0’s and  where we have 2 of something else. We
use a similar technique to count the rest of the straights, giving us a total of
where we have 2 of something else. We
use a similar technique to count the rest of the straights, giving us a total of
![( ) ( )
2[(5 ⋅94)(82- 5 - 9) - ( 5 94 + 4( 9 5⋅93))]
2 2
5 (9 ) 4
+2(9 (82- 5- 9 - 5) - 5 2 9 )
(9 )
+2(95(82- 5- 9 - 9) - 5 94) = 12964536
2](targetprobs83x.png)
So, the total is 2184813 + 12964536 = 15149349.
Back to table
Since we’re dealing in a specific suit (let’s say G(reen)), there are 3 cards of that suit (including 1 wild) for each number except 0 and 9, and there are 2 cards for those. We break it down by the length of the straight flush:
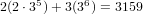 .
.
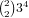 where we have
2 0’s and
where we have
2 0’s and 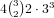 where we have 2 of something else. We use a
similar technique to count the rest of the straights, giving us a total of
where we have 2 of something else. We use a
similar technique to count the rest of the straights, giving us a total of
![[ ( ( ) ( ) ) ]
2 (2⋅34)(82- 5- 3)- 2 34 +4 3 2 ⋅33
2 2
[ 5 (3 ) 4]
+2 3 (82 - 5- 2- 3)- 5 2 3
[ (3 ) ]
+2 35(82 - 5- 3- 3)- 5 34 = 87156
2](targetprobs87x.png)
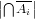 , which by de Morgan’s laws is
, which by de Morgan’s laws is 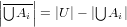 .
Now,
.
Now, 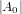 is the number of hands that don’t have a Green 0, which is
is the number of hands that don’t have a Green 0, which is
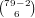 , and the other
, and the other 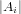 ’s are
’s are 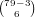 .
. 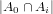 is the number of
hands that don’t have a Green 0 or a Green i, which is
is the number of
hands that don’t have a Green 0 or a Green i, which is 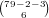 , and
the other
, and
the other 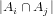 ’s are
’s are 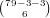 . We continue on in this manner
to find that the number of 4 card straight flushes of numbers 0-3 is
. We continue on in this manner
to find that the number of 4 card straight flushes of numbers 0-3 is
![( ) [( ) ( )] [ ( ) ( )] [ ( ) ( )] ( )
769 - 79-62 + 3 79-63 + 3 79-6 5 + 379-66 - 379-68 + 79-6 9 + 79-611 = 136161](targetprobs98x.png) (and by symmetry this is the number of 4 card straight flushes 6-9).
We use a similar technique (letting our universe of cards be all 82
cards except Green 0’s and Green 5’s) to calculate the number
of 4 card straight flushes of numbers 1-4 (and 5-8 by symmetry) is
(and by symmetry this is the number of 4 card straight flushes 6-9).
We use a similar technique (letting our universe of cards be all 82
cards except Green 0’s and Green 5’s) to calculate the number
of 4 card straight flushes of numbers 1-4 (and 5-8 by symmetry) is
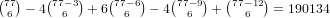 . Again, letting our
universe be all 82 cards except Green 1’s and Green 6’s, the number of 4
card straight flushes of numbers 2-5 (and 3-6 and 4-7 by symmetry) is
. Again, letting our
universe be all 82 cards except Green 1’s and Green 6’s, the number of 4
card straight flushes of numbers 2-5 (and 3-6 and 4-7 by symmetry) is
 , which gives us a total
of 2 ⋅ 136161 + 2 ⋅ 190134 + 3 ⋅ 184626 = 1206468.
, which gives us a total
of 2 ⋅ 136161 + 2 ⋅ 190134 + 3 ⋅ 184626 = 1206468.
For 0-2, our universe of cards is 82-3=79, so we get
![(79) [(79-2) (79-3)] [ (79- 5) (79-6)] (79-8)
6 - 6 + 2 6 + 2 6 + 6 - 6 = 1144050](targetprobs101x.png) , although
we have to subtract the two non-adjacent 3 card straight flushes which is
, although
we have to subtract the two non-adjacent 3 card straight flushes which is
 . (these are the same as 7-9 by symmetry) For
1-3 (and by symmetry 6-8) our universe of cards is 82-5=77, so we
get
. (these are the same as 7-9 by symmetry) For
1-3 (and by symmetry 6-8) our universe of cards is 82-5=77, so we
get 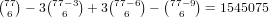 , then subtracting
, then subtracting
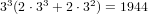 . For 2-4 (and 5-7) our universe of cards is 82-6=76,
so we get
. For 2-4 (and 5-7) our universe of cards is 82-6=76,
so we get  , then subtracting
, then subtracting
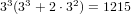 . For 3-5 (and 4-6) our universe of cards is 82-6=76, so
we get
. For 3-5 (and 4-6) our universe of cards is 82-6=76, so
we get 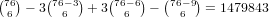 , then subtracting
, then subtracting
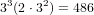 .
.
Finally, we have to add in the case where there are two non-adjacent 3 card straights. If the first straight is 0-2, the other straight could be anywhere from 4-6 to 7-9, which gives 2 ⋅ 32(3 ⋅ 33 + 2 ⋅ 32). Adding up all such cases gives an additional 2⋅32(3⋅33+2⋅32)+33(2⋅33+2⋅32)+33(33+2⋅32)+33(2⋅32) = 5427 possibilities. This gives a total of 2(1144050-1782)+2(1545075-1944)+2(1479843-1215)+2(1479843-486)+5427 = 11292195.
So, the total is 3159 + 87156 + 1206468 + 11292195 = 12588978.
Back to table
You can perhaps do some sort of inclusion-exclusion argument where your sets are
the hands that have 3 cards in any particular suit, but it gets very complicated very
fast - open to suggestions.
Back to table
You can perhaps do some sort of inclusion-exclusion argument where your sets are
the hands that have 4 cards in any particular suit, but it gets very complicated very
fast - open to suggestions.
Back to table
We can make two pair by all the possibilities under Full House, plus the following:
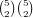 for the choices of the cards of number 0 and 9, 8 choices
for the other number, and
for the choices of the cards of number 0 and 9, 8 choices
for the other number, and  choices for the cards of that number.
If we use only one of 0 and 9, there are 2 choices for which one
to use,
choices for the cards of that number.
If we use only one of 0 and 9, there are 2 choices for which one
to use, 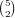 choices for the cards of that number,
choices for the cards of that number, 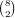 choices
for the other two numbers, and
choices
for the other two numbers, and 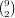 choices for the cards in each
number. If we use neither 0 nor 9, there are
choices for the cards in each
number. If we use neither 0 nor 9, there are  choices for the
numbers and
choices for the
numbers and 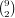 for the cards in each number. This gives a total of
for the cards in each number. This gives a total of
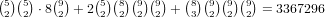 .
.
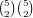 possibilities
for those cards. For the other two cards, they can’t be 0 or 9, so there
are
possibilities
for those cards. For the other two cards, they can’t be 0 or 9, so there
are 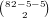 choices, except
choices, except  of these lead to another pair, so we
subtract them. Similarly, if we use one of 0 and 9, there are
of these lead to another pair, so we
subtract them. Similarly, if we use one of 0 and 9, there are 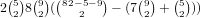 choices and if we use neither 0 nor 9 there are
choices and if we use neither 0 nor 9 there are  for a total of
for a total of 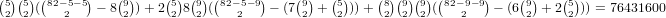 .
.So, the total is 12646280 + 3367296 + 76431600 = 92445176.
Back to table
We break it down by the number of cards of the same number:
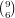 ways to choose the cards of that
number for a total of
ways to choose the cards of that
number for a total of 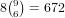 .
.
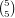 ways to choose the
cards of that number and 82-5 ways to choose the other card. Otherwise,
there are
ways to choose the
cards of that number and 82-5 ways to choose the other card. Otherwise,
there are  ways to choose the cards of that number and 82 - 9 (to
avoid picking the same number again) to choose the other card. This gives
a total of
ways to choose the cards of that number and 82 - 9 (to
avoid picking the same number again) to choose the other card. This gives
a total of 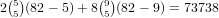 .
.
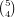 ways to choose
the cards of that number and
ways to choose
the cards of that number and  ways to choose the other card.
Otherwise, there are
ways to choose the other card.
Otherwise, there are 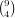 ways to choose the cards of that number
and
ways to choose the cards of that number
and 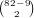 ways to choose the other card. This gives a total of
ways to choose the other card. This gives a total of
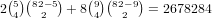 .
.
 ways to choose the cards of that number and
ways to choose the cards of that number and 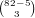 ways to
choose the other cards, but we have to subtract off the number of ways
to choose another 3 of a kind, which is
ways to
choose the other cards, but we have to subtract off the number of ways
to choose another 3 of a kind, which is 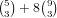 . Otherwise, there
are
. Otherwise, there
are 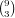 ways to choose the cards of that number and
ways to choose the cards of that number and 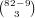 ways to
choose the other cards, but again we subtract
ways to
choose the other cards, but again we subtract 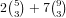 , which is the
number of ways to choose another 3 of a kind. This gives us a total of
, which is the
number of ways to choose another 3 of a kind. This gives us a total of
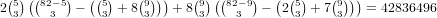 .
.So, the total is 672 + 73738 + 2678284 + 211108 + 42836496 = 45800298.
Back to table
We break it down by the distribution of cards in the full house:
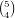 ways to choose the cards in that
number and
ways to choose the cards in that
number and 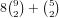 ways to choose the cards in the other number.
If the number of the 4 cards is not 0 or 9, there are 8 choices for the
number,
ways to choose the cards in the other number.
If the number of the 4 cards is not 0 or 9, there are 8 choices for the
number, 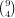 ways to choose the cards in that number and
ways to choose the cards in that number and  ways to choose the cards in the other number. This gives a total of
ways to choose the cards in the other number. This gives a total of
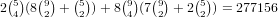 .
.
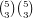 choices. If one of the numbers is 0 or 9, there are
choices. If one of the numbers is 0 or 9, there are 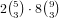 choices. If neither number is 0 nor 9, there are
choices. If neither number is 0 nor 9, there are 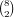 ways to choose
the numbers, so there are
ways to choose
the numbers, so there are 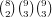 choices. All together, this gives
choices. All together, this gives
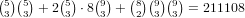 .
.
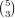 choices for the cards in that
number, and
choices for the cards in that
number, and 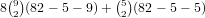 for the other 3 cards. If
the number of the 3 cards is not 0 or 9, there are 8 choices for the number,
for the other 3 cards. If
the number of the 3 cards is not 0 or 9, there are 8 choices for the number,
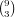 choices for the cards in that number, and
choices for the cards in that number, and 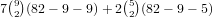 choices for the other 3 cards. All together, this gives
choices for the other 3 cards. All together, this gives 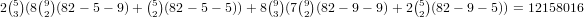 .
.So, the total is 277156 + 211108 + 12158016 = 12646280.
Back to table
We break it down by the number of odd cards:
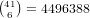 possibilities.
possibilities.
 possibilities.
possibilities.This gives a total of 4496388 + 30725318 = 35221706.
Back to table
Since there are 41 even cards and 41 odd cards, by symmetry this is the same
number as 5 odd cards, which is 35221706.
Back to table
We break it down by the lowest two cards in the hand:
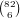 total hands,
total hands, 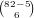 hands that have no 0 cards,
and
hands that have no 0 cards,
and 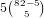 hands with only 1 0, so the number of hands that have 0 and
0 as their lowest cards is
hands with only 1 0, so the number of hands that have 0 and
0 as their lowest cards is 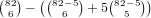 . Of these, the only
hands that don’t have 3 cards totalling ≤ 4 are those that only have 5’s
or higher for the remaining cards, and there are
. Of these, the only
hands that don’t have 3 cards totalling ≤ 4 are those that only have 5’s
or higher for the remaining cards, and there are 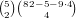 of these,
so our total is
of these,
so our total is  .
.
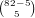 , and
, and 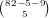 have no 1’s, so the number
of these hands is
have no 1’s, so the number
of these hands is 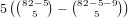 . Of these, the only hands that
don’t have 3 cards totalling ≤ 4 are those that only have 4’s or higher for
the remaining cards, and there are
. Of these, the only hands that
don’t have 3 cards totalling ≤ 4 are those that only have 4’s or higher for
the remaining cards, and there are 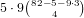 of these, so our total
is
of these, so our total
is  .
.
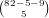 ,
and
,
and 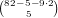 have no 1’s, so the number of these hands is
have no 1’s, so the number of these hands is
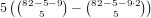 . Of these, the only hands that don’t have
3 cards totalling ≤ 4 are those that only have 3’s or higher for the
remaining cards, and there are
. Of these, the only hands that don’t have
3 cards totalling ≤ 4 are those that only have 3’s or higher for the
remaining cards, and there are 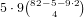 of these, so our total is
of these, so our total is
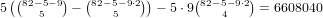 .
.
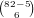 hands that have no 0’s, but
hands that have no 0’s, but 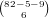 of
these hands have no 1’s, and
of
these hands have no 1’s, and  of these hands have exactly
1 1. So, there are
of these hands have exactly
1 1. So, there are 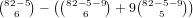 hands that have 1
and 1 as their lowest cards. Of these, the only hands that don’t have
3 cards totalling ≤ 4 are those that only have 3’s or higher for the
remaining cards, and there are
hands that have 1
and 1 as their lowest cards. Of these, the only hands that don’t have
3 cards totalling ≤ 4 are those that only have 3’s or higher for the
remaining cards, and there are 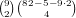 of these, so our total is
of these, so our total is
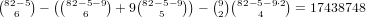 .
.Therefore, the total number is 13266257 + 36304935 + 6608040 + 17438748 = 73617980.
Back to table
By symmetry this is the same number as 3 cards totalling ≥ 4, which is
73617980.
Back to table
A skip straight is a 4 card straight where there’s a 1 number gap between each card:
i.e. 0 2 4 6, 1 3 5 7, etc.
We break it down by the length of the skip straight:
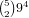 possibilities, and if there are 2 of
anything else there are
possibilities, and if there are 2 of
anything else there are 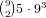 possibilities. This gives us a total of
possibilities. This gives us a total of
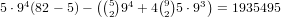 , and by symmetry the
same total for 1 3 5 7 9.
, and by symmetry the
same total for 1 3 5 7 9.
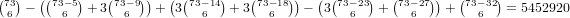 .
.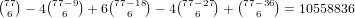 .
.So, our total is 2 ⋅ 1935495 + 2 ⋅ 5452920 + 2 ⋅ 10558836 = 35894502.
Back to table
A mixed straight is a 4 card straight in which each of the cards is a different suit. I’m
open to suggestions on how to count this efficiently.
Back to table
This page was generated from the LATEXsource with TeX4ht.