



Next: Definitions
Up: Basic Number Theory
Previous: Basic Number Theory
Contents
- Weak Mathematical Induction: If the following two things can be shown
about a proposition
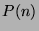 :
:
- Base Case:
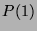 is true.
is true.
- Induction Step: If
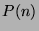 is true, then
is true, then 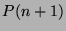 is true.
is true.
then 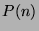 is true
is true
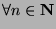 .
.
- Strong Mathematical Induction: If the following two things can be shown
about a proposition
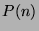 :
:
- Base Case:
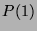 is true.
is true.
- Induction Step: If
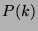 is true
is true
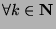 ,
, 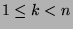 , then
, then 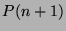 is true.
is true.
then 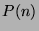 is true
is true
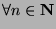 .
.
- Pigeonhole Principle: If there are
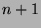 pigeons and they are put in
pigeons and they are put in
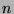 pigeonholes, then there is a pigeonhole that contains at least two pigeons.
pigeonholes, then there is a pigeonhole that contains at least two pigeons.
- Well Ordering Principle (WOP): If
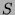 is a non-empty set that is a
subset of the positive integers, then
is a non-empty set that is a
subset of the positive integers, then 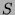 has a least element.
has a least element.
- Transitivity: If
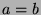 and
and 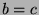 , then
, then  .
.
- Substitution: If
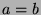 , then
, then 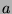 can be substituted for
can be substituted for 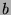 in any statement
without changing the veracity(truthfulness) of the statement.
in any statement
without changing the veracity(truthfulness) of the statement.
- Distributive Property:
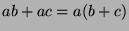 .
.
Gregory Stoll
2000-04-08
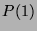 is true.
is true.
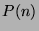 is true, then
is true, then 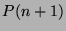 is true.
is true.
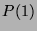 is true.
is true.
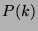 is true
is true
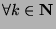 ,
, 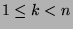 , then
, then 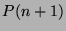 is true.
is true.